Normal Distribution Worksheet 12.7 Made Easy

Understanding normal distribution is a crucial aspect of statistics, and with the right resources, it can be made easy. In this article, we will delve into the world of normal distribution, exploring its definition, properties, and how to work with it using a worksheet.

What is Normal Distribution?

Normal distribution, also known as the Gaussian distribution or bell curve, is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean. In a normal distribution, about 68% of the data falls within one standard deviation of the mean, about 95% falls within two standard deviations, and about 99.7% falls within three standard deviations.

Properties of Normal Distribution

A normal distribution has several key properties that make it a powerful tool for statistical analysis:

• Symmetry: The normal distribution is symmetric about the mean.
• Mean: The mean of the normal distribution is the average value of the data.
• Standard Deviation: The standard deviation of the normal distribution is a measure of the spread of the data.
• Skewness: The normal distribution is not skewed, meaning that it is not asymmetrical.
• Kurtosis: The normal distribution has a kurtosis of 3, which means that it is not too peaked or too flat.

Worksheet 12.7: Normal Distribution Made Easy

To help you understand normal distribution better, let's work through a worksheet. This worksheet will guide you through the process of calculating the mean, standard deviation, and z-scores for a set of data.

Problem 1: Calculating the Mean

Calculate the mean of the following set of data: 2, 4, 6, 8, 10

Solution

To calculate the mean, add up all the values and divide by the number of values:

Mean = (2 + 4 + 6 + 8 + 10) / 5 Mean = 30 / 5 Mean = 6

Problem 2: Calculating the Standard Deviation

Calculate the standard deviation of the following set of data: 2, 4, 6, 8, 10

Solution

To calculate the standard deviation, first calculate the variance:

Variance = Σ(xi - μ)² / (n - 1) Variance = [(2 - 6)² + (4 - 6)² + (6 - 6)² + (8 - 6)² + (10 - 6)²] / (5 - 1) Variance = [16 + 4 + 0 + 4 + 16] / 4 Variance = 40 / 4 Variance = 10

Then, take the square root of the variance to get the standard deviation:

Standard Deviation = √10 Standard Deviation ≈ 3.16

Problem 3: Calculating Z-Scores

Calculate the z-scores for the following set of data: 2, 4, 6, 8, 10

Solution

To calculate the z-scores, use the following formula:

Z = (xi - μ) / σ

Where xi is the individual data point, μ is the mean, and σ is the standard deviation.

Z1 = (2 - 6) / 3.16 Z1 ≈ -1.27

Z2 = (4 - 6) / 3.16 Z2 ≈ -0.63

Z3 = (6 - 6) / 3.16 Z3 = 0

Z4 = (8 - 6) / 3.16 Z4 ≈ 0.63

Z5 = (10 - 6) / 3.16 Z5 ≈ 1.27

Interpreting Z-Scores

Z-scores can be used to determine the number of standard deviations an individual data point is away from the mean. A z-score of 0 means that the data point is equal to the mean. A positive z-score means that the data point is above the mean, while a negative z-score means that the data point is below the mean.

Normal Distribution Table

A normal distribution table, also known as a z-table, is a table that shows the area under the normal curve to the left of a given z-score. This table can be used to find the probability of a z-score being less than or equal to a given value.

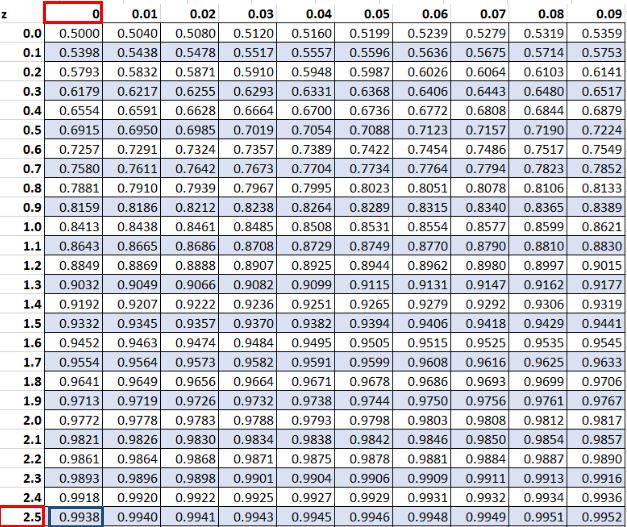
Conclusion

Normal distribution is a powerful tool for statistical analysis, and with the right resources, it can be made easy. By understanding the properties of normal distribution and how to calculate the mean, standard deviation, and z-scores, you can become proficient in using normal distribution to analyze data.