Master 12.7 Normal Distribution With 7 Essential Practice Worksheets

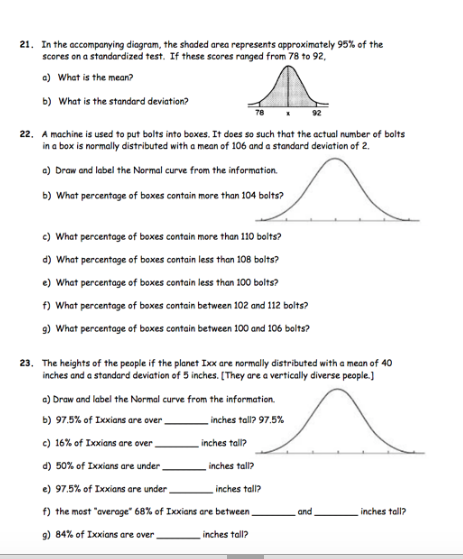
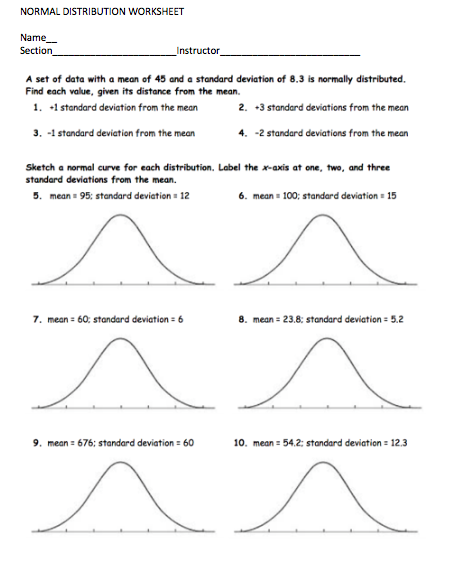
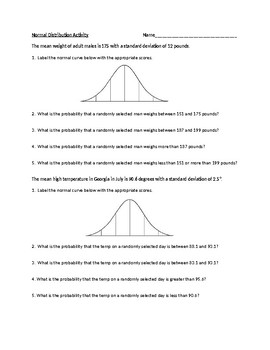
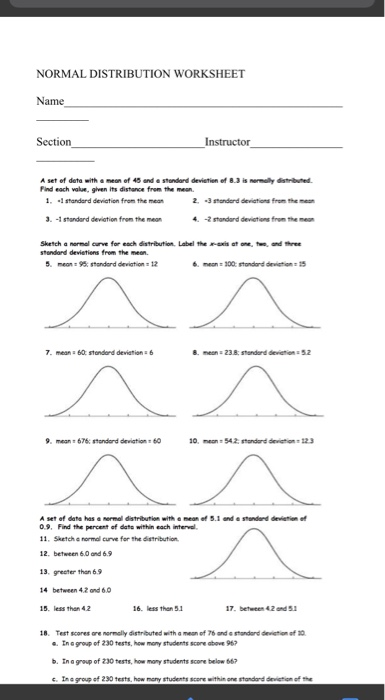
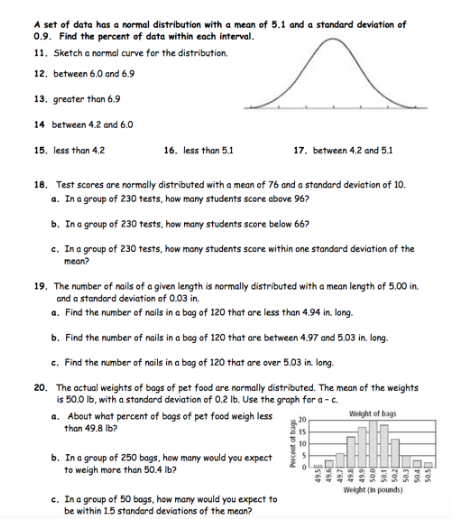
Mastering the normal distribution is a fundamental concept in statistics and data analysis. It's a crucial tool for understanding and working with data that follows a bell-curve pattern. In this article, we'll delve into the world of normal distribution, exploring its definition, properties, and applications. To help you reinforce your understanding, we'll also provide 7 essential practice worksheets to test your skills.

What is Normal Distribution?

Normal distribution, also known as the Gaussian distribution or bell curve, is a probability distribution that describes how data points are dispersed around a central value, called the mean. It's characterized by a symmetrical, bell-shaped curve, where the majority of data points cluster around the mean, and the frequency of data points decreases as you move away from the mean.

Properties of Normal Distribution

A normal distribution has several key properties:

• Symmetry: The normal distribution is symmetrical around the mean, meaning that the left and right sides of the curve are mirror images of each other.
• Mean: The mean is the central value of the distribution, which is the average value of all data points.
• Standard Deviation: The standard deviation measures the spread or dispersion of the data points from the mean.
• Skewness: The normal distribution is not skewed, meaning that it's not asymmetrical or biased towards one side.

Importance of Normal Distribution

Normal distribution plays a vital role in various fields, including:

• Statistics: Normal distribution is used to model and analyze data in statistics, helping to understand the underlying patterns and trends.
• Engineering: Normal distribution is used in engineering to model and analyze complex systems, such as control systems and signal processing.
• Finance: Normal distribution is used in finance to model and analyze stock prices, returns, and other financial data.
• Medicine: Normal distribution is used in medicine to model and analyze data related to health outcomes, such as blood pressure and cholesterol levels.

7 Essential Practice Worksheets

To help you master normal distribution, we've created 7 essential practice worksheets. These worksheets cover a range of topics, from basic concepts to more advanced applications.

Worksheet 1: Understanding Normal Distribution

• Question 1: What is the mean of a normal distribution?
• Question 2: What is the standard deviation of a normal distribution?
• Question 3: What is the skewness of a normal distribution?

Answers:

• Question 1: The mean of a normal distribution is the central value of the distribution.
• Question 2: The standard deviation of a normal distribution measures the spread or dispersion of the data points from the mean.
• Question 3: The skewness of a normal distribution is zero, meaning that it's not asymmetrical or biased towards one side.

Worksheet 2: Calculating Mean and Standard Deviation

• Question 1: Given a set of data points, calculate the mean.
• Question 2: Given a set of data points, calculate the standard deviation.

Example:

Data points: 2, 4, 6, 8, 10

• Question 1: Calculate the mean.

Answer:

Mean = (2 + 4 + 6 + 8 + 10) / 5 = 6

• Question 2: Calculate the standard deviation.

Answer:

Standard Deviation = √[(2-6)^2 + (4-6)^2 + (6-6)^2 + (8-6)^2 + (10-6)^2] / 5 = 2.82

Worksheet 3: Understanding Z-Scores

• Question 1: What is a z-score?
• Question 2: Given a data point and a mean, calculate the z-score.

Example:

Data point: 8 Mean: 6 Standard Deviation: 2

• Question 1: What is a z-score?

Answer:

A z-score measures the number of standard deviations a data point is away from the mean.

• Question 2: Calculate the z-score.

Answer:

Z-Score = (8 - 6) / 2 = 1

Worksheet 4: Working with Normal Distribution Tables

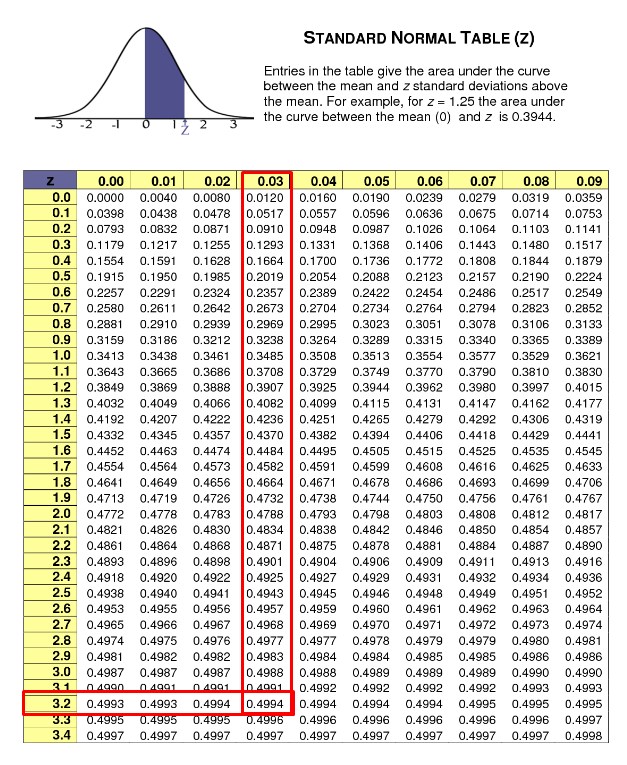
• Question 1: Given a z-score, find the corresponding probability using a normal distribution table.
• Question 2: Given a probability, find the corresponding z-score using a normal distribution table.

Example:

• Question 1: Find the probability corresponding to a z-score of 1.5.

Answer:

Using a normal distribution table, the probability corresponding to a z-score of 1.5 is 0.9332.

• Question 2: Find the z-score corresponding to a probability of 0.25.

Answer:

Using a normal distribution table, the z-score corresponding to a probability of 0.25 is -0.67.

Worksheet 5: Applying Normal Distribution to Real-World Scenarios

• Question 1: A company produces light bulbs with an average lifespan of 1000 hours and a standard deviation of 100 hours. What is the probability that a light bulb will last more than 1200 hours?
• Question 2: A medical study found that the average blood pressure of a population is 120 mmHg with a standard deviation of 10 mmHg. What is the probability that a person's blood pressure will be higher than 140 mmHg?

Answers:

• Question 1: Using the normal distribution, the probability that a light bulb will last more than 1200 hours is 0.0228.
• Question 2: Using the normal distribution, the probability that a person's blood pressure will be higher than 140 mmHg is 0.1587.

Worksheet 6: Comparing Normal Distributions

• Question 1: Compare two normal distributions with different means and standard deviations.
• Question 2: Determine which normal distribution has a higher probability of a data point being within 1 standard deviation of the mean.

Example:

Distribution 1: Mean = 10, Standard Deviation = 2 Distribution 2: Mean = 12, Standard Deviation = 3

• Question 1: Compare the two normal distributions.

Answer:

Distribution 1 has a higher probability of a data point being within 1 standard deviation of the mean.

• Question 2: Determine which normal distribution has a higher probability of a data point being within 1 standard deviation of the mean.

Answer:

Distribution 1 has a higher probability of a data point being within 1 standard deviation of the mean.

Worksheet 7: Advanced Applications of Normal Distribution

• Question 1: Use the normal distribution to model and analyze a complex system.
• Question 2: Use the normal distribution to make predictions about future data points.

Example:

• Question 1: Use the normal distribution to model and analyze the stock prices of a company.

Answer:

Using historical data, the normal distribution can be used to model and analyze the stock prices of the company.

• Question 2: Use the normal distribution to make predictions about future stock prices.

Answer:

Using the normal distribution, predictions can be made about future stock prices based on historical data.

Gallery of Normal Distribution:

FAQs:

We hope this comprehensive guide to normal distribution has helped you master this essential concept in statistics and data analysis. Remember to practice with our 7 essential worksheets to reinforce your understanding.

Gallery of Master 12.7 Normal Distribution With 7 Essential Practice Worksheets