
Matrices are a fundamental concept in linear algebra, and finding the determinant of a matrix is a crucial operation in many mathematical and real-world applications. In this article, we will explore the concept of determinants, specifically for 3x3 matrices, and provide a comprehensive worksheet with examples to help you practice and reinforce your understanding.
What is a Determinant?
The determinant of a matrix is a scalar value that represents certain properties of the matrix. It can be thought of as a measure of the "volume" of the parallelepiped spanned by the column vectors of the matrix. The determinant is denoted as det(A) or |A|, where A is the matrix.
Determinant of a 3x3 Matrix
To calculate the determinant of a 3x3 matrix, we can use the following formula:
det(A) = a(ei − fh) − b(di − fg) + c(dh − eg)
where a, b, c, d, e, f, g, h, and i are the elements of the matrix A.
Step-by-Step Process
To find the determinant of a 3x3 matrix, follow these steps:
- Write down the matrix and identify the elements.
- Multiply the elements of the first row by the corresponding elements of the second and third rows.
- Calculate the sum of the products from step 2.
- Repeat steps 2 and 3 for the second and third rows.
- Apply the formula det(A) = a(ei − fh) − b(di − fg) + c(dh − eg).
Worksheet with Examples
Here are some examples to help you practice finding the determinant of a 3x3 matrix:
Example 1
Find the determinant of the matrix:
| 1 2 3 |
| 4 5 6 |
| 7 8 9 |
Solution
Using the formula, we get:
det(A) = 1(5(9) − 6(8)) − 2(4(9) − 6(7)) + 3(4(8) − 5(7)) = 1(45 − 48) − 2(36 − 42) + 3(32 − 35) = 1(-3) − 2(-6) + 3(-3) = -3 + 12 − 9 = 0
Example 2
Find the determinant of the matrix:
| 2 1 4 |
| 3 5 2 |
| 1 3 6 |
Solution
Using the formula, we get:
det(A) = 2(5(6) − 2(3)) − 1(3(6) − 2(1)) + 4(3(3) − 5(1)) = 2(30 − 6) − 1(18 − 2) + 4(9 − 5) = 2(24) − 1(16) + 4(4) = 48 − 16 + 16 = 48
Example 3
Find the determinant of the matrix:
| 1 0 2 |
| 3 4 1 |
| 2 5 3 |
Solution
Using the formula, we get:
det(A) = 1(4(3) − 1(5)) − 0(3(3) − 1(2)) + 2(3(5) − 4(2)) = 1(12 − 5) − 0(9 − 2) + 2(15 − 8) = 1(7) − 0(7) + 2(7) = 7 + 14 = 21
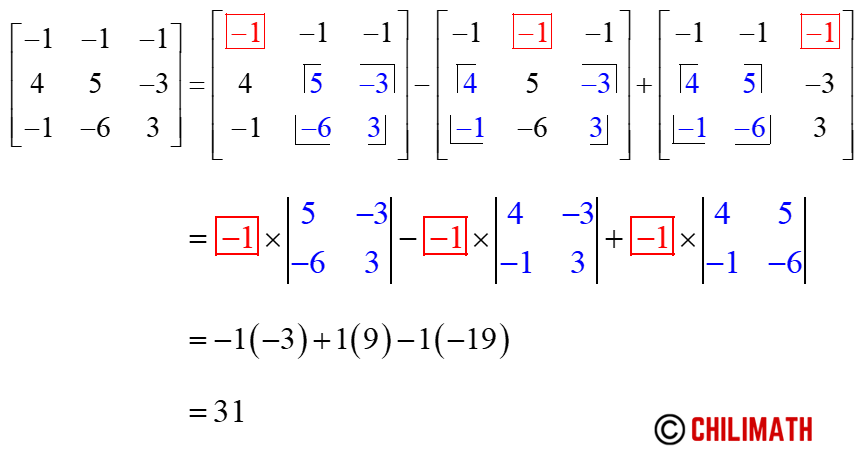
Gallery of Determinant Examples




Frequently Asked Questions
What is the determinant of a matrix?
+The determinant of a matrix is a scalar value that represents certain properties of the matrix. It can be thought of as a measure of the "volume" of the parallelepiped spanned by the column vectors of the matrix.
How do I calculate the determinant of a 3x3 matrix?
+To calculate the determinant of a 3x3 matrix, use the formula det(A) = a(ei − fh) − b(di − fg) + c(dh − eg), where a, b, c, d, e, f, g, h, and i are the elements of the matrix A.
What are some applications of determinants in real-life scenarios?
+Determinants have numerous applications in various fields, including physics, engineering, computer science, and economics. They are used to solve systems of linear equations, find the area of triangles and parallelograms, and determine the invertibility of matrices.
We hope this worksheet and examples have helped you understand the concept of determinants for 3x3 matrices. Practice makes perfect, so be sure to try out the examples and exercises to reinforce your understanding.

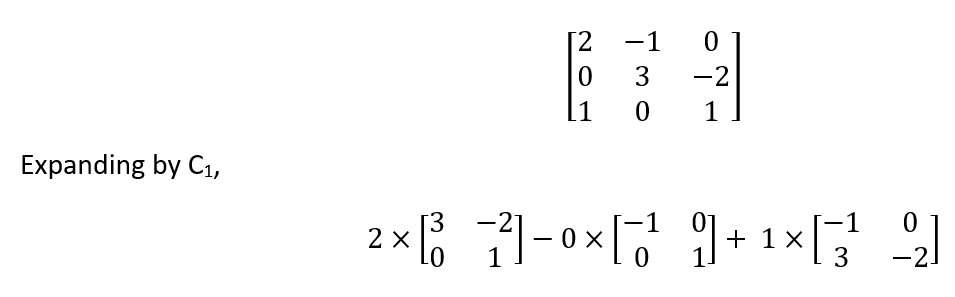





.png)

