Solving systems of equations is a fundamental problem in various fields, including physics, engineering, economics, and computer science. While there are many ways to solve systems of equations, using Excel can be an efficient and intuitive approach, especially when dealing with large systems or multiple variables. In this article, we will explore five ways to solve systems of equations in Excel, covering both linear and nonlinear systems.
Understanding Systems of Equations
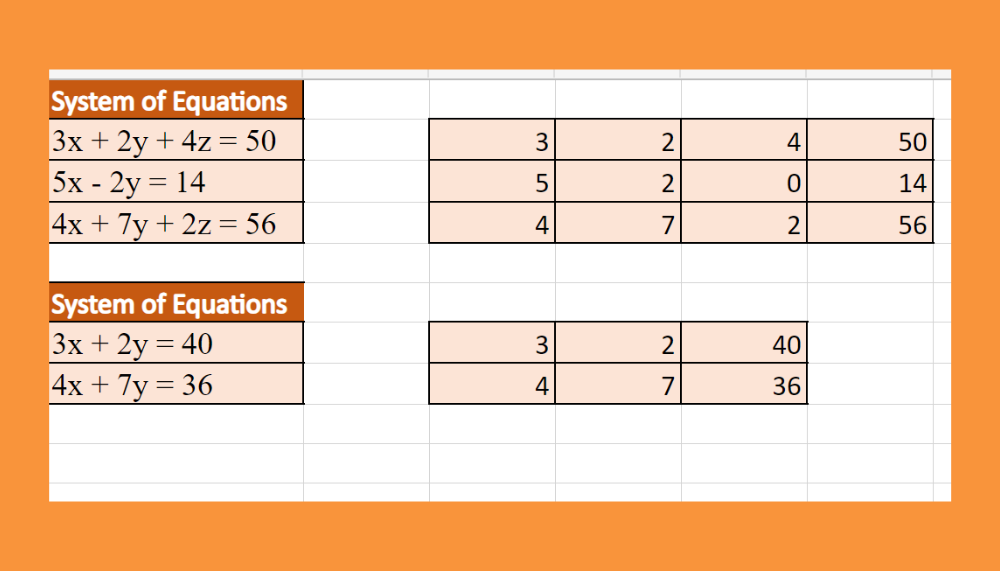
A system of equations is a collection of equations that involve multiple variables and constants. Solving a system of equations means finding the values of the variables that satisfy all the equations simultaneously. Systems of equations can be linear or nonlinear, depending on the relationships between the variables.
Linear systems of equations involve linear relationships between variables, whereas nonlinear systems involve more complex relationships, such as quadratic or polynomial relationships. Linear systems can be solved using various methods, including substitution, elimination, and matrix operations. Nonlinear systems, on the other hand, often require numerical methods or iterative approaches.
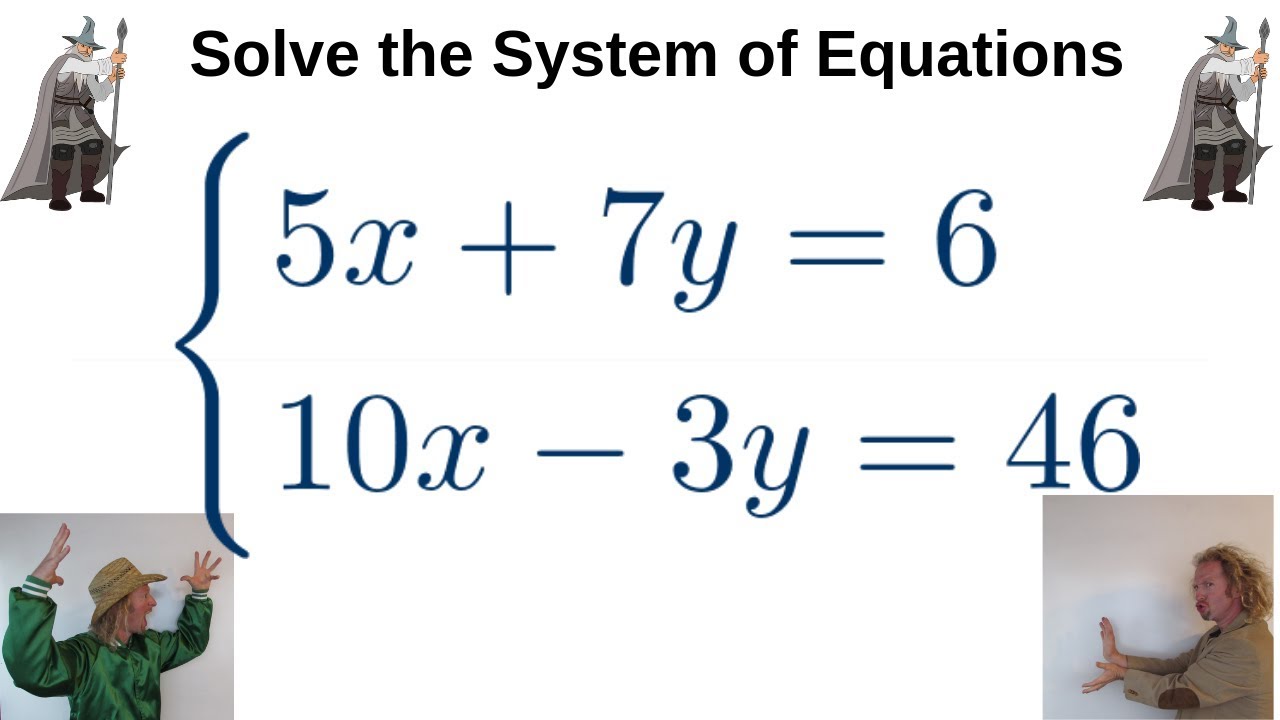
Method 1: Using Excel's Solver Add-in
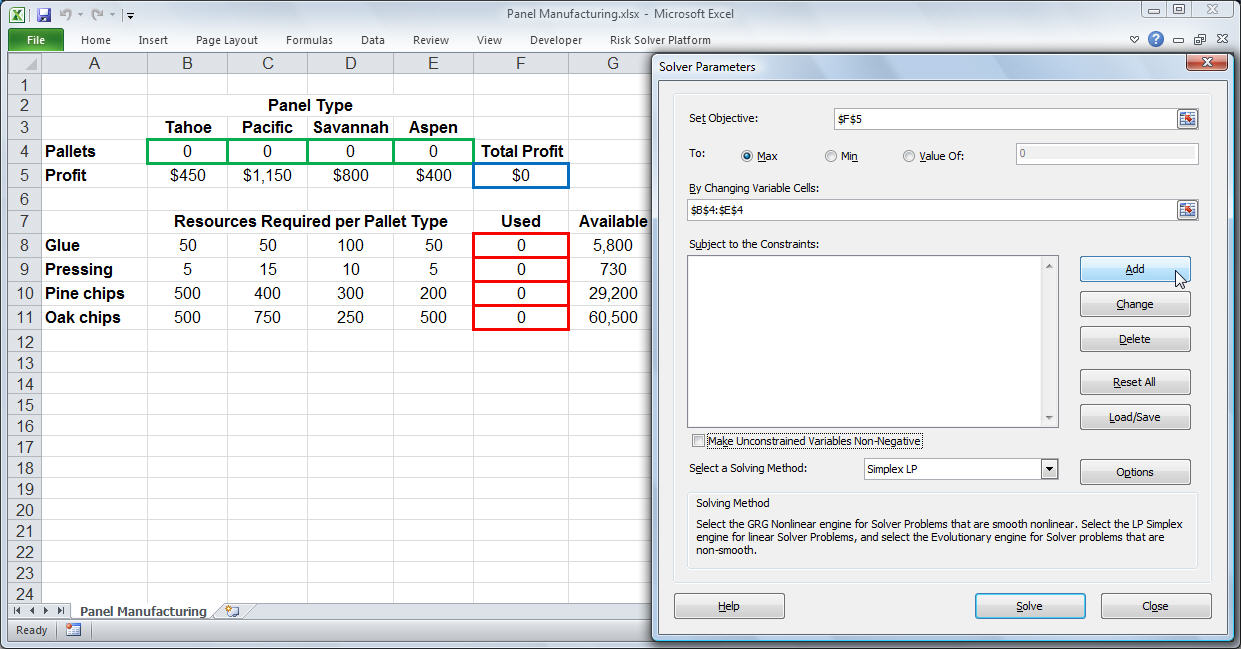
Excel's Solver add-in is a powerful tool for solving systems of equations, both linear and nonlinear. To use Solver, you need to set up the system of equations in Excel, specify the variables and constraints, and then use the Solver dialog box to find the solution.
Here's an example of how to use Solver to solve a linear system of equations:
- Set up the system of equations in Excel, using separate cells for each equation.
- Define the variables and constraints using the Solver dialog box.
- Choose the solving method (e.g., GRG Nonlinear or Simplex LP) and click Solve.
Solver will then find the solution to the system of equations and display the results in the specified cells.
Method 2: Using Matrix Operations
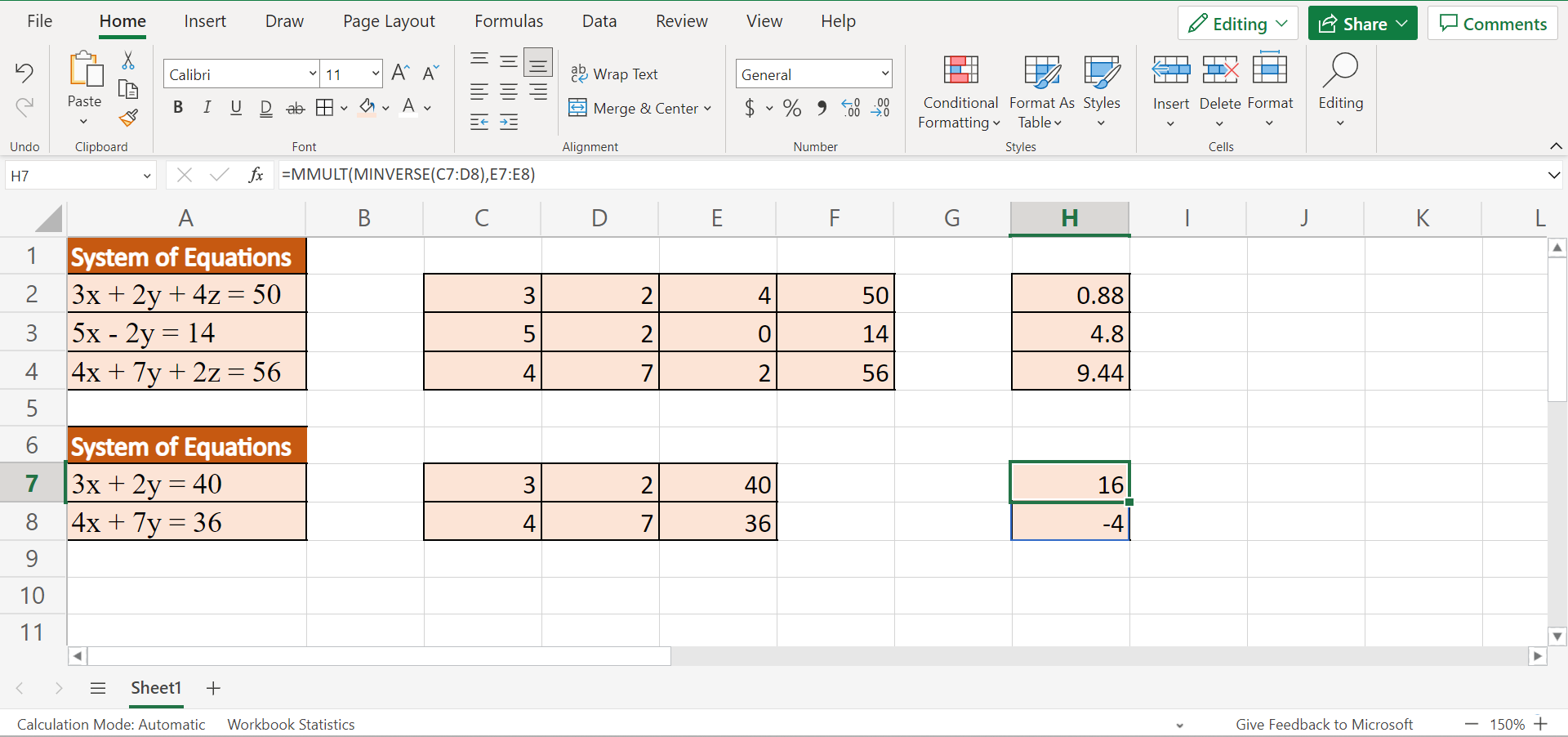
Matrix operations are a fundamental approach to solving linear systems of equations. In Excel, you can use matrix operations to solve systems of equations by representing the equations as matrices and then using matrix inversion or multiplication to find the solution.
Here's an example of how to use matrix operations to solve a linear system of equations:
- Represent the system of equations as matrices, using separate ranges for each equation.
- Use the MINVERSE function to invert the coefficient matrix.
- Multiply the inverted matrix by the constant matrix to find the solution.
For example, suppose we have the following system of equations:
2x + 3y = 7 x - 2y = -3
We can represent this system as matrices:
| 2 3 | | x | | 7 | | 1 -2 | | y | = | -3 |
Using the MINVERSE function, we can invert the coefficient matrix:
= MINVERSE(A1:B2)
This gives us the inverted matrix:
| 2 1 | | 1 0 | | 3 -2 | | 0 1 |
Multiplying this inverted matrix by the constant matrix, we get:
= MMULT(C1:D2, E1:F2)
This gives us the solution:
x = 1 y = 2

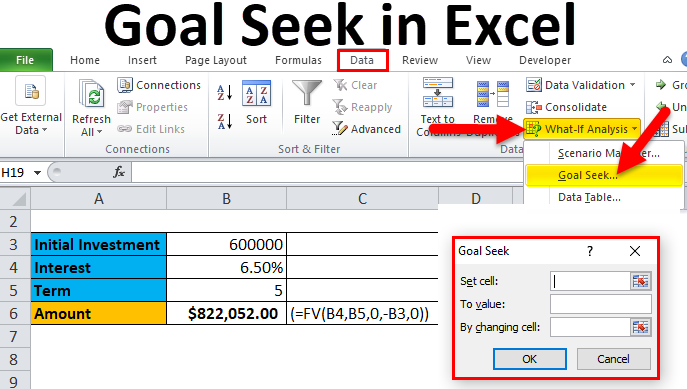
Method 3: Using the Goal Seek Function
The Goal Seek function is another useful tool in Excel for solving systems of equations. This function allows you to set a target value for a specific cell and then use iterative calculations to find the values of the variables that achieve that target.
Here's an example of how to use the Goal Seek function to solve a system of equations:
- Set up the system of equations in Excel, using separate cells for each equation.
- Choose the target cell and specify the target value.
- Use the Goal Seek dialog box to set up the iteration parameters and choose the solving method.
The Goal Seek function will then iteratively adjust the values of the variables to achieve the target value.
Method 4: Using VBA Macros
VBA macros are a powerful way to extend the functionality of Excel and automate complex calculations, including solving systems of equations. By writing a VBA macro, you can create a custom solution that uses iterative calculations or other numerical methods to solve the system of equations.
Here's an example of how to use a VBA macro to solve a system of equations:
- Set up the system of equations in Excel, using separate cells for each equation.
- Create a new VBA module and write a macro that uses iterative calculations or other numerical methods to solve the system of equations.
- Use the macro to solve the system of equations and display the results in the specified cells.

Method 5: Using Add-ins and Third-Party Software
Finally, there are many add-ins and third-party software available that can help you solve systems of equations in Excel. These tools often provide advanced functionality, such as symbolic manipulation, numerical methods, and optimization techniques, that can be used to solve complex systems of equations.
Some popular add-ins and third-party software for solving systems of equations in Excel include:
- MathType: a popular equation editor that allows you to create and solve systems of equations.
- Maple: a powerful computer algebra system that can be used to solve systems of equations symbolically or numerically.
- MATLAB: a high-level programming language and environment that provides advanced functionality for solving systems of equations.

Gallery of Excel Systems of Equations

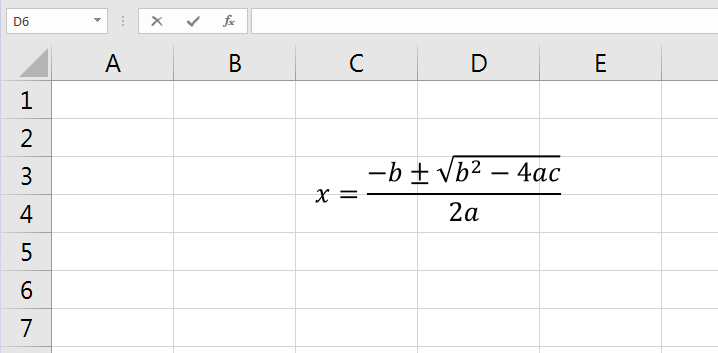


How do I solve a system of equations in Excel?
+There are several ways to solve a system of equations in Excel, including using the Solver add-in, matrix operations, the Goal Seek function, VBA macros, and add-ins and third-party software.
What is the Solver add-in in Excel?
+The Solver add-in is a powerful tool in Excel that allows you to solve systems of equations, both linear and nonlinear.
How do I use matrix operations to solve a system of equations in Excel?
+You can use matrix operations to solve a system of equations in Excel by representing the equations as matrices, inverting the coefficient matrix, and multiplying the inverted matrix by the constant matrix.
We hope this article has provided you with a comprehensive guide to solving systems of equations in Excel. Whether you are a student, a researcher, or a professional, these methods can help you solve complex systems of equations efficiently and accurately.