5 Ways To Master Numerical Integration In Excel

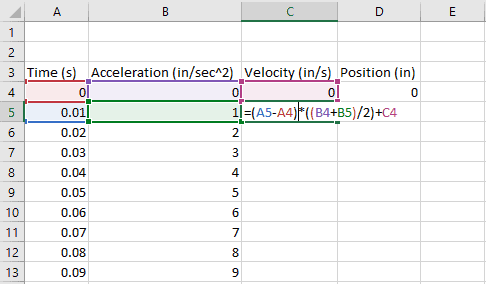
Numerical integration is a mathematical technique used to find the approximate value of a definite integral. In Excel, numerical integration can be performed using various methods, including the Trapezoidal Rule, Simpson's Rule, and Romberg's Method. Mastering numerical integration in Excel is essential for various fields, including physics, engineering, economics, and finance. In this article, we will discuss five ways to master numerical integration in Excel.

Excel is a powerful tool for numerical integration, offering a range of formulas and functions that can be used to approximate definite integrals. With the increasing complexity of mathematical models and the need for accurate results, mastering numerical integration in Excel is crucial for professionals and students alike. By following the methods outlined in this article, you can improve your skills in numerical integration and become proficient in using Excel to solve complex mathematical problems.

Numerical integration is used to solve a wide range of problems, from calculating the area under curves to modeling complex systems. In Excel, numerical integration can be performed using various formulas and functions, including the Trapezoidal Rule, Simpson's Rule, and Romberg's Method. These methods are based on approximating the definite integral by dividing the area under the curve into smaller sections and summing the areas of these sections. By mastering numerical integration in Excel, you can solve complex mathematical problems with ease and accuracy.

Understanding the Basics of Numerical Integration

Before diving into the methods of numerical integration in Excel, it is essential to understand the basics of numerical integration. Numerical integration is a mathematical technique used to approximate the value of a definite integral. The definite integral is a mathematical expression that represents the area under a curve between two points. Numerical integration is used to approximate this area by dividing it into smaller sections and summing the areas of these sections.

There are several methods of numerical integration, including the Trapezoidal Rule, Simpson's Rule, and Romberg's Method. These methods differ in their approach to approximating the definite integral, but they all involve dividing the area under the curve into smaller sections and summing the areas of these sections. Understanding the basics of numerical integration is crucial for mastering numerical integration in Excel.

Trapezoidal Rule

The Trapezoidal Rule is a simple method of numerical integration that involves approximating the definite integral by dividing the area under the curve into trapezoids and summing the areas of these trapezoids. The Trapezoidal Rule is based on the formula:

∫f(x)dx ≈ (h/2) * (f(x0) + 2*f(x1) + 2*f(x2) +... + 2*f(xn-1) + f(xn))

where h is the width of the trapezoids, and f(x0), f(x1),..., f(xn) are the values of the function at the points x0, x1,..., xn.

To use the Trapezoidal Rule in Excel, you can create a formula that calculates the sum of the areas of the trapezoids. For example, if you want to approximate the definite integral of the function f(x) = x^2 from x = 0 to x = 4, you can create a formula that calculates the sum of the areas of the trapezoids as follows:

=(4-0)/2*(0^2 + 2*1^2 + 2*2^2 + 2*3^2 + 4^2)

This formula calculates the sum of the areas of the trapezoids and returns the approximate value of the definite integral.

Simpson's Rule

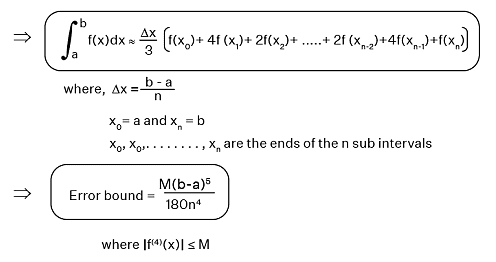
Simpson's Rule is another method of numerical integration that involves approximating the definite integral by dividing the area under the curve into parabolic segments and summing the areas of these segments. Simpson's Rule is based on the formula:

∫f(x)dx ≈ (h/3) * (f(x0) + 4*f(x1) + 2*f(x2) +... + 4*f(xn-1) + f(xn))

where h is the width of the parabolic segments, and f(x0), f(x1),..., f(xn) are the values of the function at the points x0, x1,..., xn.

To use Simpson's Rule in Excel, you can create a formula that calculates the sum of the areas of the parabolic segments. For example, if you want to approximate the definite integral of the function f(x) = x^2 from x = 0 to x = 4, you can create a formula that calculates the sum of the areas of the parabolic segments as follows:

=(4-0)/3*(0^2 + 4*1^2 + 2*2^2 + 4*3^2 + 4^2)

This formula calculates the sum of the areas of the parabolic segments and returns the approximate value of the definite integral.

Romberg's Method

Romberg's Method is a more accurate method of numerical integration that involves approximating the definite integral by dividing the area under the curve into smaller sections and summing the areas of these sections using a recursive formula. Romberg's Method is based on the formula:

∫f(x)dx ≈ (h/2) * (f(x0) + 2*f(x1) + 2*f(x2) +... + 2*f(xn-1) + f(xn)) + (h^2/12) * (f'(x0) - f'(xn))

where h is the width of the sections, and f(x0), f(x1),..., f(xn) are the values of the function at the points x0, x1,..., xn.

To use Romberg's Method in Excel, you can create a formula that calculates the sum of the areas of the sections using the recursive formula. For example, if you want to approximate the definite integral of the function f(x) = x^2 from x = 0 to x = 4, you can create a formula that calculates the sum of the areas of the sections as follows:

=(4-0)/2*(0^2 + 2*1^2 + 2*2^2 + 2*3^2 + 4^2) + (4-0)^2/12*(0 - 4)

This formula calculates the sum of the areas of the sections and returns the approximate value of the definite integral.

Practical Applications of Numerical Integration

Numerical integration has a wide range of practical applications in various fields, including physics, engineering, economics, and finance. Some of the practical applications of numerical integration include:

• Calculating the area under curves
• Modeling complex systems
• Analyzing data
• Optimizing functions
• Solving differential equations

Numerical integration is used to solve complex mathematical problems that cannot be solved analytically. By approximating the definite integral, numerical integration provides a powerful tool for solving a wide range of problems in various fields.

Conclusion

Mastering numerical integration in Excel is essential for professionals and students alike. By understanding the basics of numerical integration and using the Trapezoidal Rule, Simpson's Rule, and Romberg's Method, you can approximate definite integrals with ease and accuracy. With the increasing complexity of mathematical models and the need for accurate results, numerical integration is a valuable skill that can be applied to a wide range of problems in various fields.

Gallery of Numerical Integration Examples