In finance, statistics, and engineering, calculating variance and covariance is essential for understanding the relationships between different variables. The variance-covariance matrix, also known as the covariance matrix, is a powerful tool for analyzing the behavior of multiple variables. In this article, we will discuss the concept of variance and covariance, the importance of the variance-covariance matrix, and provide a step-by-step guide on how to calculate it in Excel.
Understanding Variance and Covariance
Variance measures the spread or dispersion of a single variable from its mean value. It calculates how much individual data points deviate from the average value. Covariance, on the other hand, measures the relationship between two variables. It calculates how much the variables move together. A positive covariance indicates that the variables tend to move in the same direction, while a negative covariance indicates that they tend to move in opposite directions.
Importance of Variance-Covariance Matrix
The variance-covariance matrix is a square matrix that summarizes the variance and covariance of multiple variables. It is essential for various applications, including:
- Portfolio optimization: The variance-covariance matrix is used to calculate the optimal portfolio weights that minimize risk.
- Risk management: It helps to identify the sources of risk and the relationships between different risk factors.
- Statistical modeling: The variance-covariance matrix is used to model complex relationships between variables.
- Data analysis: It provides insights into the underlying structure of the data.
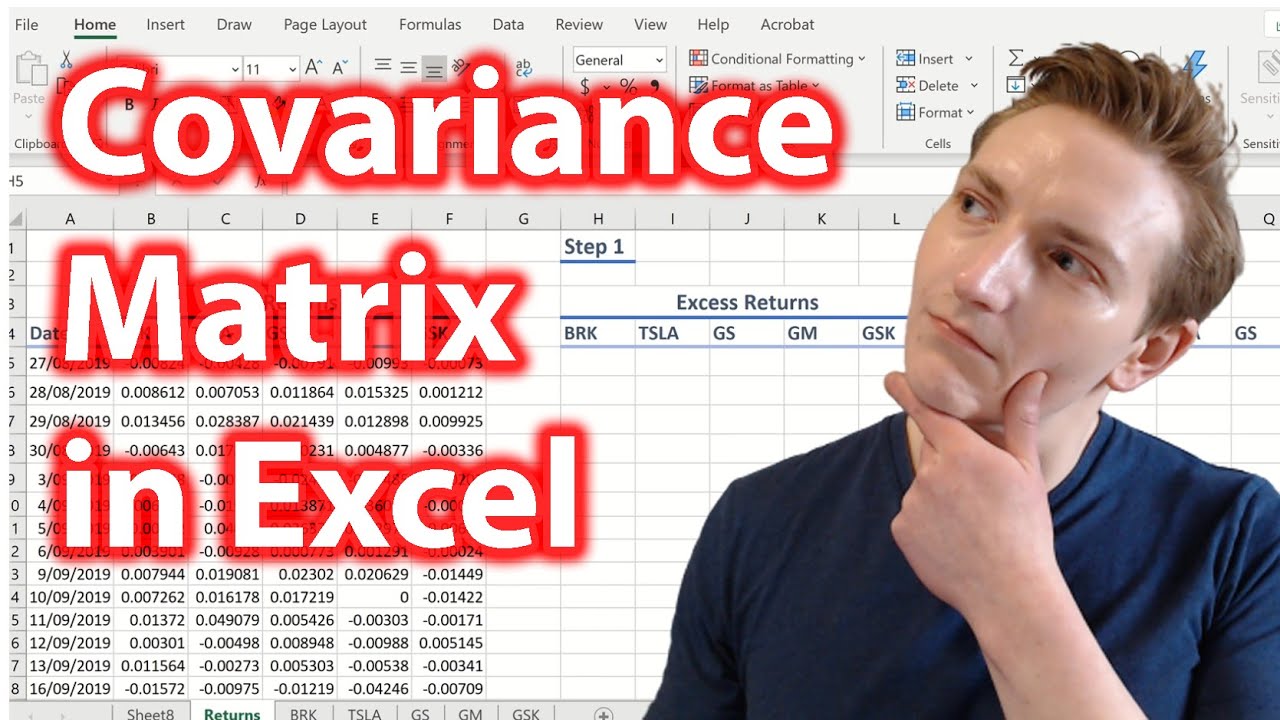
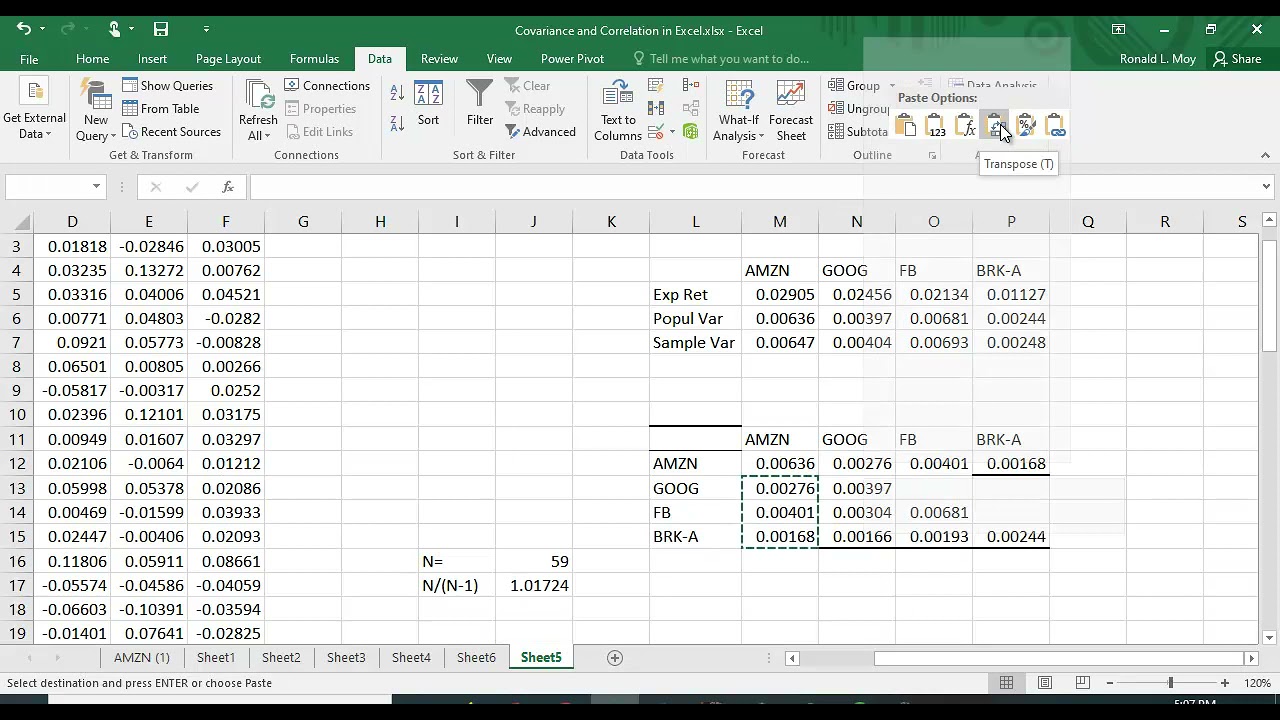
Step-by-Step Guide to Calculating Variance-Covariance Matrix in Excel
Calculating the variance-covariance matrix in Excel is a straightforward process. Here's a step-by-step guide:
Step 1: Prepare the Data
Organize your data in a table with each variable in a separate column. Ensure that the data is clean and free from errors.

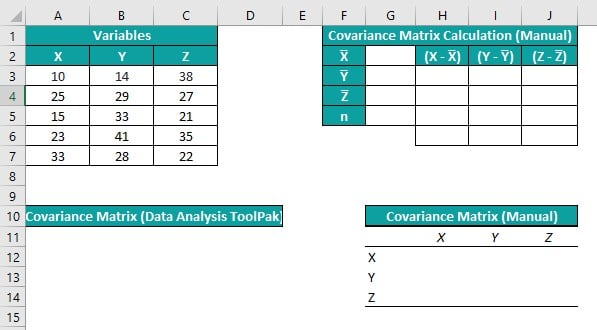
Step 2: Calculate the Mean
Calculate the mean of each variable using the AVERAGE function.

Step 3: Calculate the Deviations
Calculate the deviations of each data point from the mean using the A1-MEAN(A:A) formula, where A1 is the first data point and MEAN(A:A) is the mean of the variable.

Step 4: Calculate the Covariance
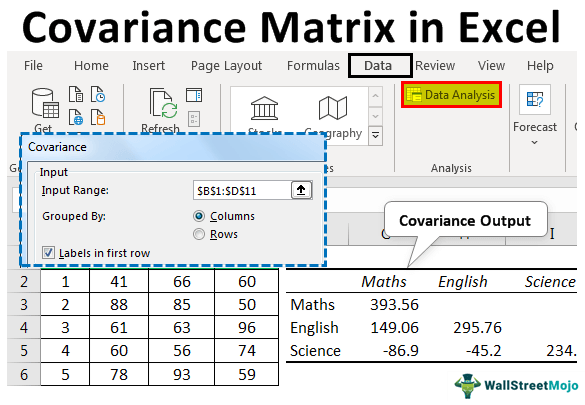
Calculate the covariance between each pair of variables using the COVAR function.

Step 5: Calculate the Variance
Calculate the variance of each variable using the VAR function.

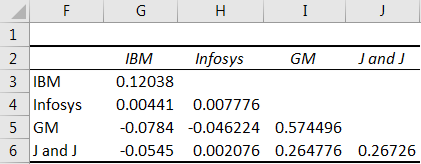
Step 6: Construct the Variance-Covariance Matrix
Construct the variance-covariance matrix by arranging the variances on the diagonal and the covariances on the off-diagonal elements.

Gallery of Variance-Covariance Matrix




FAQs
What is the purpose of the variance-covariance matrix?
+The variance-covariance matrix is used to summarize the variance and covariance of multiple variables. It is essential for portfolio optimization, risk management, statistical modeling, and data analysis.
How do I calculate the variance-covariance matrix in Excel?
+To calculate the variance-covariance matrix in Excel, you need to follow these steps: calculate the mean, calculate the deviations, calculate the covariance, calculate the variance, and construct the variance-covariance matrix.
What is the difference between variance and covariance?
+Variance measures the spread or dispersion of a single variable from its mean value. Covariance measures the relationship between two variables. It calculates how much the variables move together.
We hope this article has provided a comprehensive guide to calculating the variance-covariance matrix in Excel. By following these steps, you can easily construct the variance-covariance matrix and gain insights into the underlying structure of your data.