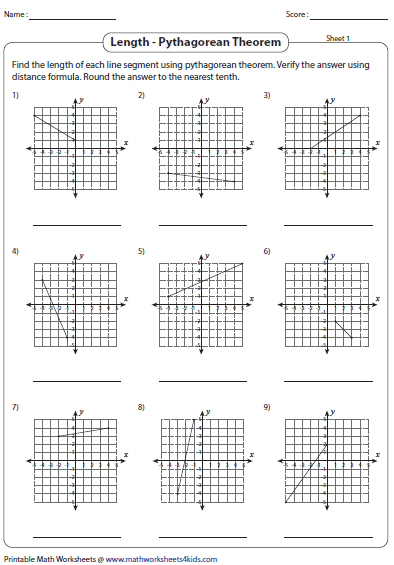
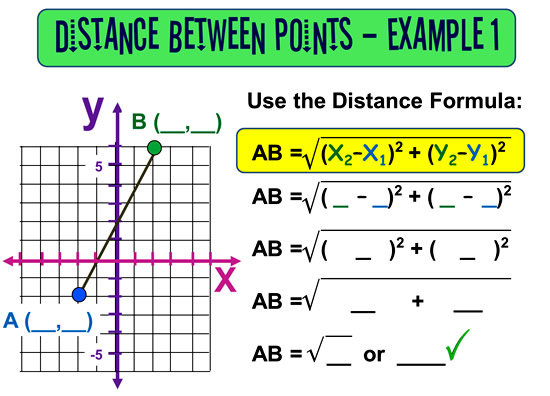
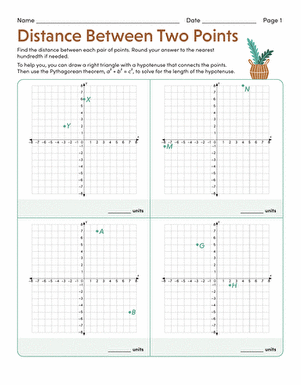
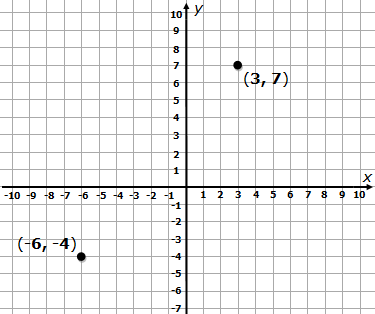The concept of distance between two points is a fundamental idea in mathematics, particularly in geometry and trigonometry. It is essential to understand how to calculate the distance between two points in a coordinate plane, as it has numerous applications in various fields, including physics, engineering, and computer science.
In this article, we will delve into the concept of distance between two points, its importance, and provide a comprehensive guide on how to calculate it using different methods. We will also include a worksheet with exercises to help you practice and reinforce your understanding of the concept.
What is the Distance Between Two Points?
The distance between two points in a coordinate plane is the length of the line segment connecting the two points. It is a measure of how far apart the two points are. In a two-dimensional coordinate system, the distance between two points can be calculated using the distance formula.
Why is the Distance Between Two Points Important?
The distance between two points has numerous applications in various fields, including:
- Physics: The distance between two objects is essential in calculating their relative motion, velocity, and acceleration.
- Engineering: The distance between two points is crucial in designing and building structures, such as bridges, roads, and buildings.
- Computer Science: The distance between two points is used in algorithms for computer graphics, game development, and geographic information systems (GIS).
- Navigation: The distance between two points is essential in navigation systems, such as GPS, to calculate the distance between two locations.
Calculating the Distance Between Two Points
There are several methods to calculate the distance between two points, including:
1. Distance Formula
The distance formula is the most common method used to calculate the distance between two points in a coordinate plane. The formula is:
d = √((x2 - x1)^2 + (y2 - y1)^2)
where (x1, y1) and (x2, y2) are the coordinates of the two points.

2. Pythagorean Theorem
The Pythagorean theorem can also be used to calculate the distance between two points. The theorem states that the square of the length of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the lengths of the other two sides.
d = √(a^2 + b^2)
where a and b are the lengths of the two sides of the right-angled triangle.

3. Distance Between Two Points on a Number Line
The distance between two points on a number line can be calculated by subtracting the smaller number from the larger number.
d = |x2 - x1|
where x1 and x2 are the coordinates of the two points.

Worksheet: Distance Between Two Points
Here are some exercises to help you practice calculating the distance between two points:
- Calculate the distance between the points (2, 3) and (4, 6) using the distance formula.
- Calculate the distance between the points (1, 2) and (3, 4) using the Pythagorean theorem.
- Calculate the distance between the points (5, 6) and (7, 8) on a number line.
- Calculate the distance between the points (2, 5) and (6, 3) using the distance formula.
- Calculate the distance between the points (1, 1) and (3, 3) using the Pythagorean theorem.




Frequently Asked Questions
What is the distance formula?
+The distance formula is a mathematical formula used to calculate the distance between two points in a coordinate plane. The formula is: d = √((x2 - x1)^2 + (y2 - y1)^2)
How do I calculate the distance between two points on a number line?
+The distance between two points on a number line can be calculated by subtracting the smaller number from the larger number. The formula is: d = |x2 - x1|
What is the Pythagorean theorem?
+The Pythagorean theorem is a mathematical theorem that states that the square of the length of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the lengths of the other two sides. The formula is: d = √(a^2 + b^2)
We hope this article has provided you with a comprehensive guide on how to calculate the distance between two points. Remember to practice regularly and use the worksheet provided to reinforce your understanding of the concept. If you have any questions or need further clarification, please don't hesitate to ask.