5 Ways To Apply Chebyshevs Theorem In Excel

The concept of Chebyshev's Theorem may seem daunting, but its application in Excel can be surprisingly straightforward. Chebyshev's Theorem, named after the Russian mathematician Pafnuty Chebyshev, is a statistical concept that describes the probability of a dataset falling within a certain number of standard deviations from the mean. In this article, we will explore five practical ways to apply Chebyshev's Theorem in Excel, making it easier for you to work with data and make informed decisions.

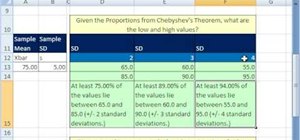
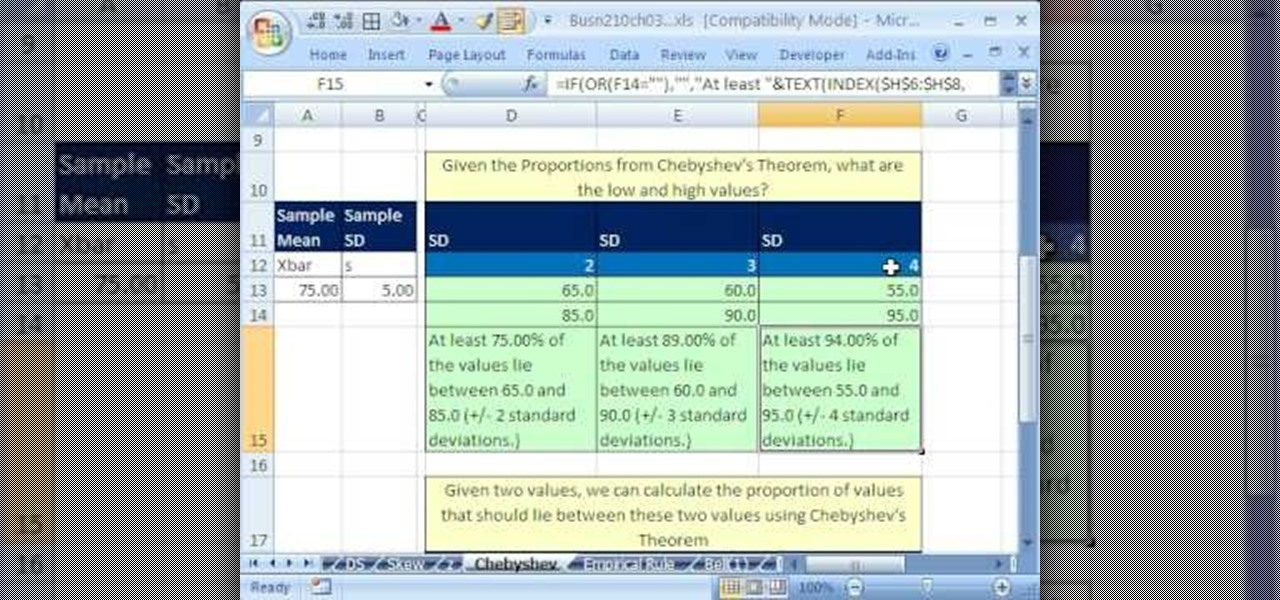
Chebyshev's Theorem states that for any dataset, at least (1 - 1/k^2) of the data points fall within k standard deviations from the mean, where k is a positive integer. This theorem has far-reaching implications in statistics, engineering, and data analysis. By applying Chebyshev's Theorem in Excel, you can better understand the distribution of your data, identify potential outliers, and make more accurate predictions.

1. Calculating the Percentage of Data Points within a Certain Range

One of the most straightforward applications of Chebyshev's Theorem in Excel is to calculate the percentage of data points that fall within a certain range. For example, suppose you have a dataset of exam scores, and you want to know what percentage of students scored within two standard deviations of the mean.

Using Chebyshev's Theorem, you can calculate the percentage of data points that fall within two standard deviations of the mean as follows:

= (1 - 1/2^2) * 100%

This formula returns the percentage of data points that fall within two standard deviations of the mean, which is approximately 75%.

2. Identifying Outliers in a Dataset

Chebyshev's Theorem can also be used to identify potential outliers in a dataset. By calculating the number of standard deviations from the mean, you can determine whether a data point is likely to be an outlier.

For example, suppose you have a dataset of stock prices, and you want to identify any potential outliers. You can use the following formula to calculate the number of standard deviations from the mean:

= (x - mean) / stdev

Where x is the data point, mean is the average value of the dataset, and stdev is the standard deviation of the dataset.

If the result is greater than 2 or 3 standard deviations from the mean, it may indicate that the data point is an outlier.

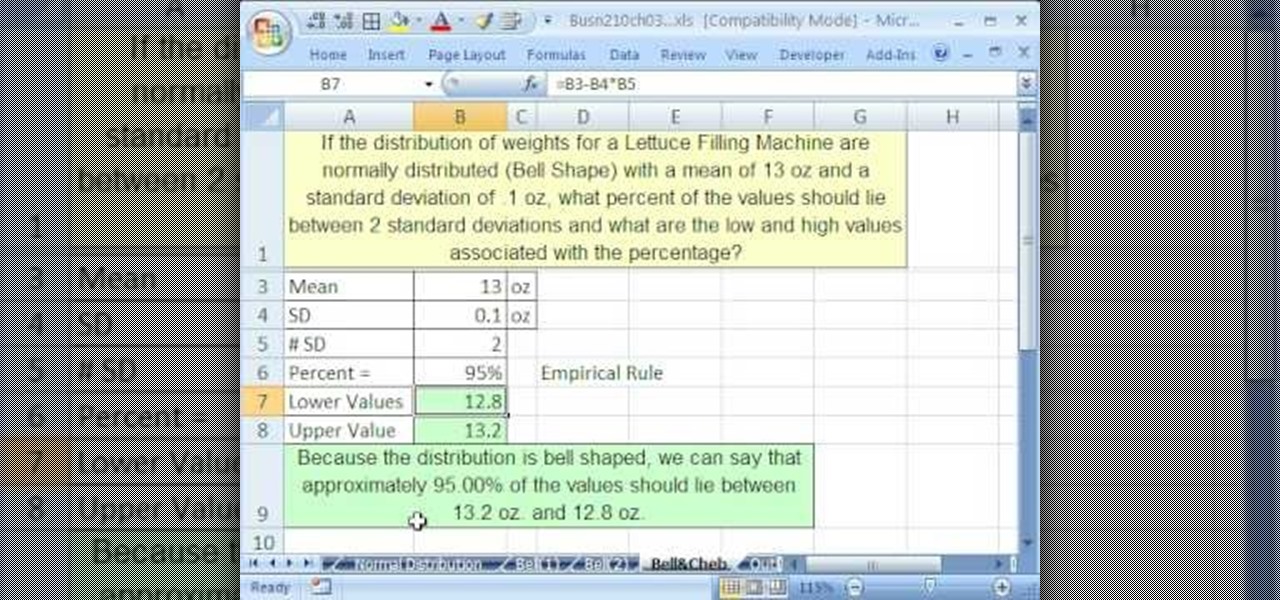
3. Creating a Histogram with Chebyshev's Theorem

A histogram is a graphical representation of a dataset that shows the distribution of values. By applying Chebyshev's Theorem, you can create a histogram that highlights the percentage of data points that fall within a certain range.

For example, suppose you have a dataset of customer ages, and you want to create a histogram that shows the distribution of ages. You can use the following steps to create a histogram with Chebyshev's Theorem:

Calculate the mean and standard deviation of the dataset.
Use Chebyshev's Theorem to calculate the percentage of data points that fall within a certain range (e.g., two standard deviations from the mean).
Create a histogram with bins that correspond to the calculated range.
Use the histogram to visualize the distribution of data points within the calculated range.

4. Predicting Future Values with Chebyshev's Theorem

Chebyshev's Theorem can also be used to predict future values based on past data. By analyzing the distribution of past data, you can estimate the likelihood of future values falling within a certain range.

For example, suppose you have a dataset of sales data, and you want to predict future sales based on past trends. You can use the following steps to predict future values with Chebyshev's Theorem:

Calculate the mean and standard deviation of the past sales data.
Use Chebyshev's Theorem to calculate the percentage of past sales that fell within a certain range (e.g., two standard deviations from the mean).
Estimate the future sales based on the calculated range.
Use the estimated future sales to inform business decisions.

5. Comparing Distributions with Chebyshev's Theorem

Finally, Chebyshev's Theorem can be used to compare the distributions of two or more datasets. By analyzing the distribution of each dataset, you can determine whether they are similar or different.

For example, suppose you have two datasets of exam scores, one from a previous year and one from the current year. You can use the following steps to compare the distributions with Chebyshev's Theorem:

Calculate the mean and standard deviation of each dataset.
Use Chebyshev's Theorem to calculate the percentage of data points that fall within a certain range (e.g., two standard deviations from the mean) for each dataset.
Compare the calculated percentages to determine whether the distributions are similar or different.
Use the comparison to inform decisions about curriculum changes or teaching methods.

Gallery of Chebyshev's Theorem

Frequently Asked Questions

What is Chebyshev's Theorem?

Chebyshev's Theorem is a statistical concept that describes the probability of a dataset falling within a certain number of standard deviations from the mean.

How can I apply Chebyshev's Theorem in Excel?

You can apply Chebyshev's Theorem in Excel by using formulas to calculate the percentage of data points that fall within a certain range, identifying outliers, creating histograms, predicting future values, and comparing distributions.

What are the limitations of Chebyshev's Theorem?

Chebyshev's Theorem has several limitations, including that it only provides a lower bound for the probability of a dataset falling within a certain range, and it does not provide any information about the shape of the distribution.

In conclusion, Chebyshev's Theorem is a powerful statistical concept that can be applied in a variety of ways in Excel. By using formulas to calculate the percentage of data points that fall within a certain range, identifying outliers, creating histograms, predicting future values, and comparing distributions, you can gain a deeper understanding of your data and make more informed decisions.