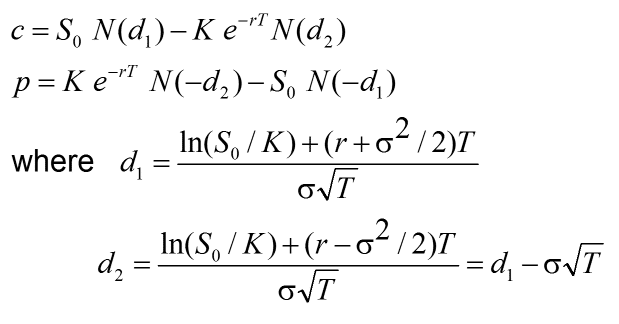Black Scholes Model In Excel Made Easy

The Black Scholes model is a widely used financial model that estimates the value of a call option or a put option. The model is named after the economists Fischer Black and Myron Scholes, who first introduced it in the 1970s. In this article, we will explain how to implement the Black Scholes model in Excel, making it easy for anyone to use.

Understanding the Black Scholes Model

Before we dive into the implementation, let's take a brief look at the underlying theory. The Black Scholes model is based on the following assumptions:

The stock price follows a geometric Brownian motion.
The risk-free interest rate is constant.
The volatility of the stock price is constant.
There are no dividends or other distributions.

The model uses the following inputs:

S: the current stock price.
K: the strike price of the option.
T: the time to expiration of the option.
r: the risk-free interest rate.
σ: the volatility of the stock price.

With these inputs, the Black Scholes model calculates the value of the call option (C) or the put option (P).

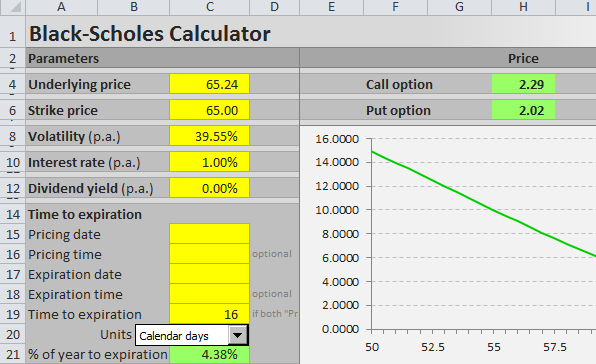
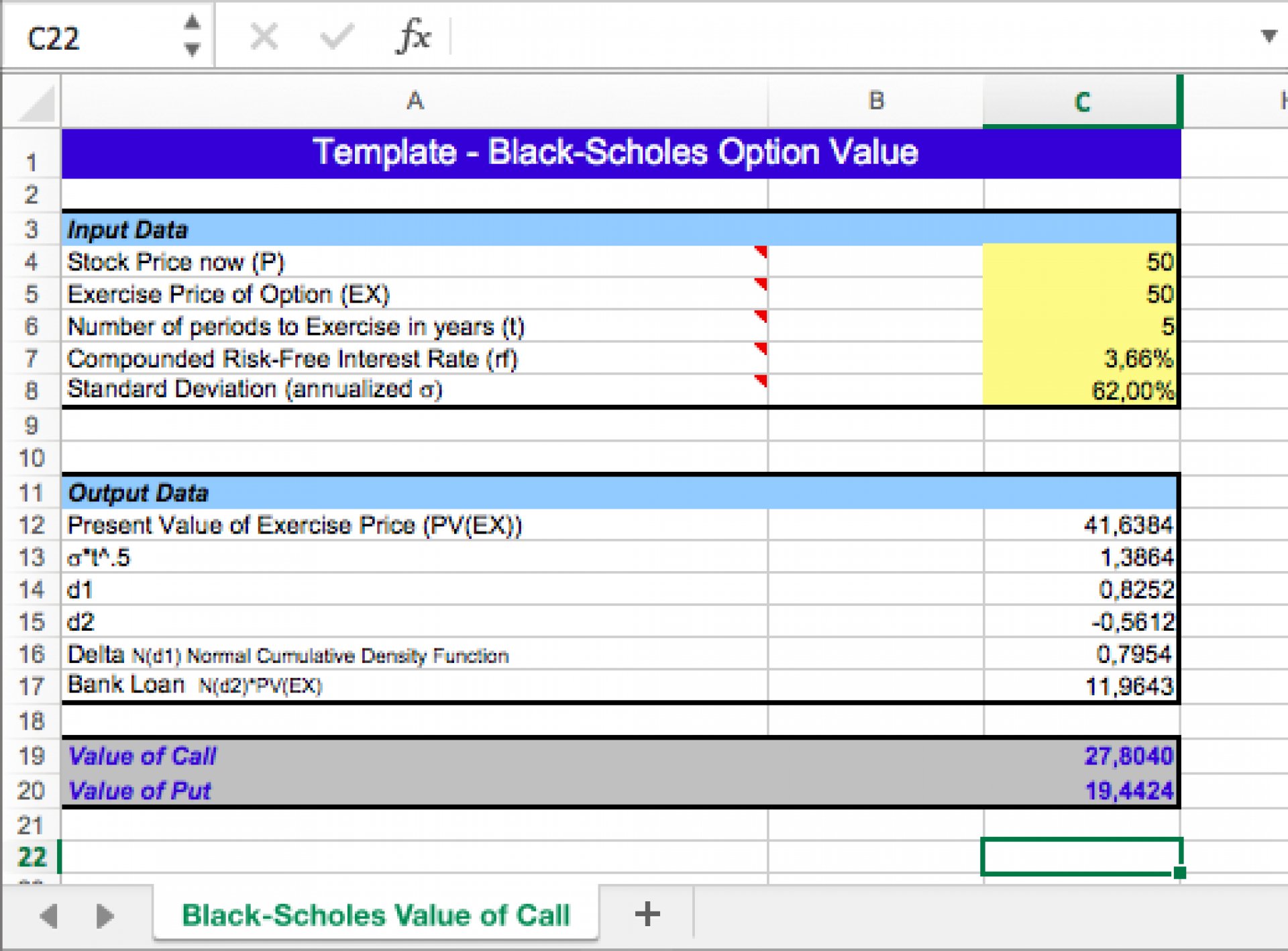
Implementing the Black Scholes Model in Excel

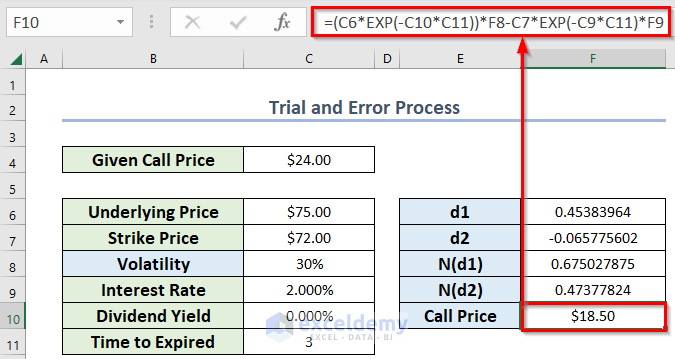
To implement the Black Scholes model in Excel, we will use the following formulas:

d1 = (ln(S/K) + (r + σ^2/2)T) / (σ√T)
d2 = d1 - σ√T
C = S * N(d1) - K * e^(-rT) * N(d2)
P = K * e^(-rT) * N(-d2) - S * N(-d1)

Where N(x) is the cumulative distribution function of the standard normal distribution.

Let's create a simple Excel spreadsheet to calculate the value of a call option and a put option using the Black Scholes model.

In the spreadsheet, we will use the following cells:

A1: S (current stock price)
B1: K (strike price of the option)
C1: T (time to expiration of the option)
D1: r (risk-free interest rate)
E1: σ (volatility of the stock price)
F1: d1 (calculated using the formula)
G1: d2 (calculated using the formula)
H1: C (value of the call option)
I1: P (value of the put option)

Using the Formulas

Now, let's enter the formulas into the spreadsheet:

F1: =((LN(A1/B1) + (D1 + E1^2/2)C1) / (E1SQRT(C1)))
G1: =F1 - E1*SQRT(C1)
H1: =A1NORM.S.DIST(F1,TRUE) - B1EXP(-D1*C1)*NORM.S.DIST(G1,TRUE)
I1: =B1EXP(-D1C1)NORM.S.DIST(-G1,TRUE) - A1NORM.S.DIST(-F1,TRUE)

Where NORM.S.DIST(x,TRUE) is the cumulative distribution function of the standard normal distribution.

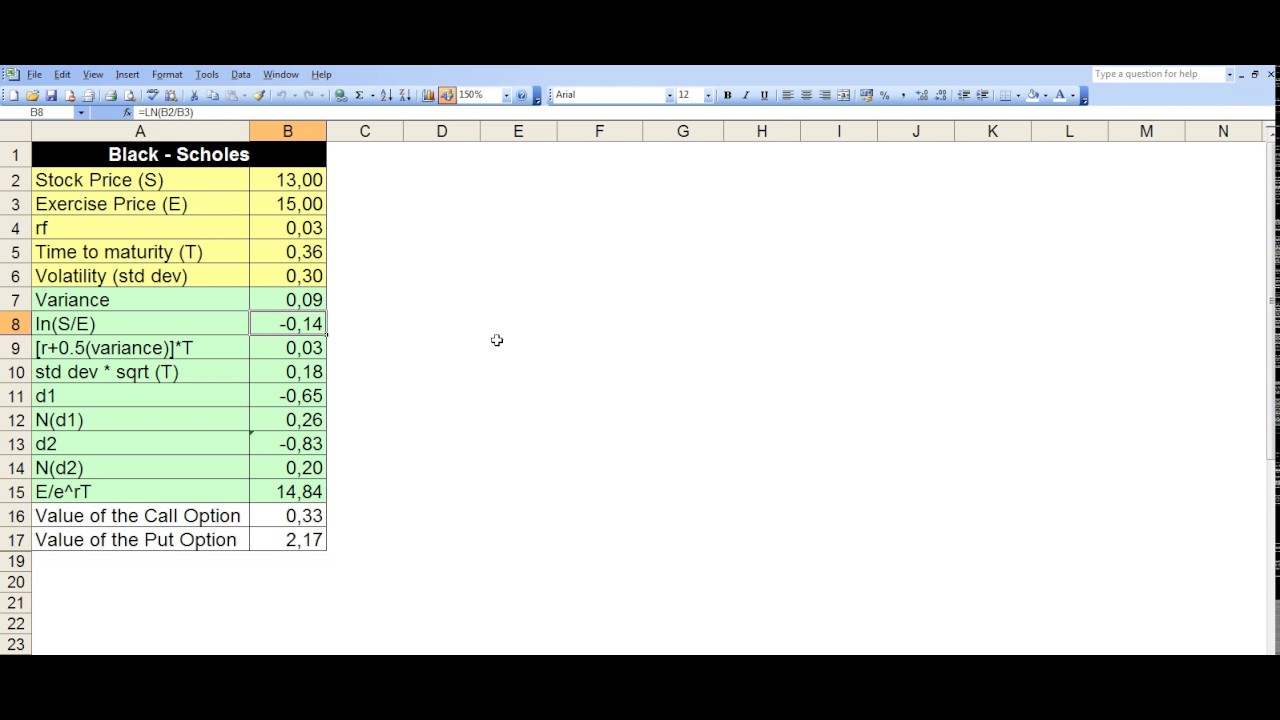
Example

Let's use an example to illustrate the calculation.

Assume we have the following inputs:

S = 100 (current stock price)
K = 110 (strike price of the option)
T = 1 (time to expiration of the option)
r = 0.05 (risk-free interest rate)
σ = 0.2 (volatility of the stock price)

Using the formulas, we calculate the value of the call option and the put option:

d1 = 0.1852
d2 = -0.0148
C = 6.7555
P = 2.9119

So, the value of the call option is approximately 6.76, and the value of the put option is approximately 2.91.

Conclusion

The Black Scholes model is a widely used financial model that estimates the value of a call option or a put option. In this article, we explained how to implement the Black Scholes model in Excel, making it easy for anyone to use. We used formulas to calculate the value of the call option and the put option, and provided an example to illustrate the calculation.

Remember to use the correct inputs and formulas to get accurate results.

Gallery of Black Scholes Model

What is the Black Scholes model?

The Black Scholes model is a financial model that estimates the value of a call option or a put option.

What are the inputs of the Black Scholes model?

The inputs of the Black Scholes model are the current stock price, the strike price of the option, the time to expiration of the option, the risk-free interest rate, and the volatility of the stock price.